:(
Kiniaa: Udowodnij, że w trójkącie ABC symetralna boku BC przecina dwusieczną kąta BAC w punkcie B
leżącym na okręgu opisanym na trójkącie ABC.
24 maj 15:14
Godzio:
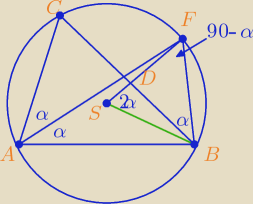
Zadanie sprowadza się do udowodnienia, że |∡SDB| = |∡SDC| = 90
o
Trzeba pamiętać, że środkiem okręgu opisanego na trójkącie jest punkt przecięcia się
symetralnych boków trójkąta.
|∡BAC| = 2α
W trójkącie SBF mamy:
|∡BSF| = 2α
|∡SFB| = |∡FBS| = 90 − α
|∡CBF| = |∡CAF| = α bo są to kąty oparte na tym samym łuku
|∡BDF| = 180 − (90 − α) − α = 90
o
Co oznacza że prosta SF jest symetralną odcinka CB co kończy dowód
24 maj 16:13
Kiniaa: Ale dlaczego akurat mamy udowodnić że |∡SDB| = |∡SDC| = 90 stopni

? Przecież ja mam
udowodnić, że symetralna boku BC przecina dwusieczną kąta BAC w punkcie F.
Więc nie rozumiem.
25 maj 20:46
Kiniaa: 
25 maj 21:07
Godzio:
Jeśli tam jest kąt prosty to udowodnisz, że prosta SF jest symetralną

25 maj 21:47
Kiniaa: ale ja nie mam udowodnić że SF jest symetralną tylko że przecina dwusieczną w punkcie F.
25 maj 22:13
Godzio:
No dobra, inaczej
Poprowadziłem dwusieczną kąta BAC, z środa okręgu poprowadziłem promień do punktu przecięcia
się dwusiecznej z okręgiem, jeśli udowodnię, że symetralna zawiera ten promień to pokaże to co
trzeba udowodnić, a symetralna zawiera ten promień tylko wtedy, gdy promień jest prostopadły
do boku BC
25 maj 22:15
s:
24 wrz 19:03
 Zadanie sprowadza się do udowodnienia, że |∡SDB| = |∡SDC| = 90o
Trzeba pamiętać, że środkiem okręgu opisanego na trójkącie jest punkt przecięcia się
symetralnych boków trójkąta.
|∡BAC| = 2α
W trójkącie SBF mamy:
|∡BSF| = 2α
|∡SFB| = |∡FBS| = 90 − α
|∡CBF| = |∡CAF| = α bo są to kąty oparte na tym samym łuku
|∡BDF| = 180 − (90 − α) − α = 90o
Co oznacza że prosta SF jest symetralną odcinka CB co kończy dowód
Zadanie sprowadza się do udowodnienia, że |∡SDB| = |∡SDC| = 90o
Trzeba pamiętać, że środkiem okręgu opisanego na trójkącie jest punkt przecięcia się
symetralnych boków trójkąta.
|∡BAC| = 2α
W trójkącie SBF mamy:
|∡BSF| = 2α
|∡SFB| = |∡FBS| = 90 − α
|∡CBF| = |∡CAF| = α bo są to kąty oparte na tym samym łuku
|∡BDF| = 180 − (90 − α) − α = 90o
Co oznacza że prosta SF jest symetralną odcinka CB co kończy dowód
 ? Przecież ja mam
udowodnić, że symetralna boku BC przecina dwusieczną kąta BAC w punkcie F.
Więc nie rozumiem.
? Przecież ja mam
udowodnić, że symetralna boku BC przecina dwusieczną kąta BAC w punkcie F.
Więc nie rozumiem.

